1.2 算法和算法的表示

1.2.4 几种常用算法介绍

关于算法的研究可参阅有关的书籍，本书不可能罗列所有算法。这里只介绍几个典型算法，目的是使读者了解一些解题的基本思想和方法，了解如何设计算法。在本书后续各章中，我们将结合C语言的具体内容和实际应用问题进一步讨论算法的设计。

1.枚举法
　　枚举法也称为穷举法，它的基本思想是：首先根据问题的部分条件预估答案的范围，然后在此范围内对所有可能的情况进行逐一验证，直到全部情况均通过了验证为止。若某个情况使验证符合题目的全部条件，则该情况为本题的一个答案；若全部情况验证结果均不符合题目的全部条件，则说明该题无答案。

　　在实际应用问题中，许多问题需要用穷举法来解决。中国古代数学家张丘建在他的《算经》中曾提出著名的"百钱百鸡问题"，其题目如下：
　　例题1-4： 鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一；百钱买百鸡，翁、母、雏各几何？
　　这就是一个典型的枚举问题。如果用x、y、z分别代表公鸡、母鸡、小鸡的数量，根据题意列方程：

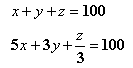　　据题意可知，x、y、z的范围一定是0到100的正整数，那么，最简单的解题方法是：假设一组x、y、z的值，直接带入方程组求解，即在各个变量的取值范围内不断变化x、y、z的值，穷举x、y、z 全部可能的组合，若满足方程组则是一组解。这样即可得到问题的全部解。
可见，利用枚举法解题需要以下步骤：
　　(1) 分析题目，确定答案的大致范围。
　　(2) 确定列举方法。常用的列举方法有：顺序列举，排列列举和组合列举。
　　(3) 作试验，直到遍历所有情况。
　　(4) 试验完后可能找到与题目要求完全一致的一组或多组答案，也可能没找到答案，即证明题目无答案。
　　枚举法的特点是算法简单，容易理解，但运算量较大。对于可确定取值范围但又找不到其它更好的算法时，就可以用枚举法。通常枚举法用来解决"有几种组合"、"是否存在"、求解不定方程等类型的问题。利用枚举法设计算法大多以循环控制结构实现。

2.迭代法
　　迭代法是一种数值近似求解的方法，在科学计算领域中，许多问题需要用这种方法解决。迭代法的特点是：把一个复杂问题的求解过程转化为相对简单的迭代算式，然后重复执行这个简单的算式，直到得到最终解。
　　迭代法有精确迭代法和近似迭代法。所谓精确迭代是指算法本身提供了问题的精确解。如对N个数求和、求均值、求方差等，这些问题都适合使用精确迭代法解决。

　　例1-5： 计算S=1+2+3+4+…+100
　　其迭代方法如下：
　　首先确定迭代变量S的初始值为0；
　　其次确定迭代公式s+i→s；
　　当i分别取值1，2，3，4，…，100时，重复计算迭代公式s+i→s，迭代100次后，即可求出S的精确值。
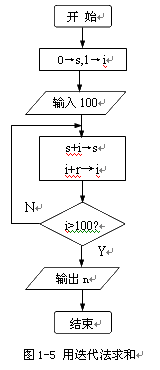
　　其中，i的取值是一个有序数列，所以可以由计数器产生，即使i的初始值为1，然后每迭代一次就对i加1。图1-5是用迭代法求和的流程图。
　　迭代法的应用更主要的是数值的近似求解，它既可以用来求解代数方程，又可以用来求解微分方程。在科学计算领域，人们时常会遇到求微分方程的数值解或解方程f(x)=0等计算问题。这些问题无法用求和或求均值那样的直接求解方法。例如，一般的一元五次或更高次方程、几乎所有的超越方程以及描述电磁波运动规律的麦克斯韦方程等，它们的解都无法用解析方法表达出来。为此，人们只能用数值计算的方法求出问题的近似解，而解的误差是人们可以估计和控制的。
　　我们以求解方程f(x)=0为例说明近似迭代法的基本方法。首先把求解方程变换成为迭代算式x=g(x)，然后由估计的一个根的初始近似值X0出发，应用迭代计算公式xk+1=g(xk)求出另一个近似值X1，再由X1确定X2，…，最终构造出一个序列X0，X1，X2，…，Xn，…，就可逐次逼近方程的根。

　　例1-6：求方程x3-x-1=0在x=1.5附近的一个根。
　　首先将方程改写成：

　　用给定的初始近似值X0=1.5代入上式的右端，得到:

　　再用X1作为近似值代入(1)式的右端，又得到:

　　按这种方法重复以上步骤，可以逐次求得更精确的值。这一过程即为迭代过程。显然，迭代过程就是通过原值求出新值，再用新值替代原值的过程。
　　对于一个收敛的迭代过程，从理论上讲，虽然经无限多次迭代可以得到准确解，但实际计算时，只能迭代有限次，这就是计算机执行算法的有穷性特征。
　　由以上分析可见，使用近似迭代法构造算法的基本方法是：首先确定一个合适的迭代公式，选取一个初始近似值以及解的误差，然后用循环处理实现迭代过程，终止循环过程的条件是前后两次得到的近似值之差的绝对值小于或等于预先给定的误差。并认为最后一次迭代得到的近似值为问题的解。
迭代法通常用于非数值运算的求解问题。

3.递推和递归法
　　这是程序设计中常用的两种算法，都是利用某些公式的递推性。最常见的例子是计算级数，一般给出数列后项与前项的递推公式，要求计算数列通项。例如：
　　（1）f1(n)=2+ f1(n-1)，f1(1)=1 f1(n)={1，3，5，7，…}
　　这是首项为1公差为2的等差数列（等差级数）。
　　（2）f2(n)=2 f2(n-1)，f2(1)=1 f2(n)={1，2，4，8，…}
　　这是首项为1公比为2的等比数列。
　　（3）f3(n)=n f3(n-1)，f3(1)=1 f3(n)={1，2，6，24，…}
　　这个数列的通项f3(n)=n!。
　　（1）f4(n)= f4(n-1)+ f4(n-2)，f4(1)=1，f4(2)=1 f4(n)={1，1，2，3，…}
　　这就是有名的斐波那契数列。
　　以上数列的共同特点是，在数列的未知项与已知项之间存在着一定关系，借助于已知项和这一关系，就可逐项求出未知项。计算这些数列通常用递推和递归两种算法。
　　递推法：
　　所谓递推法，是指利用递推公式，由简到繁逐次迭代求解，

　　例1-7：求n！，设n=15。
　　求解n！可由1！+2！+，…，n！来完成，其算法存在如下递推过程：
　　f(0)=0!=1
　　f(1)=1!=1 0! =1
　　f(2)=2!=2 1! =2
　　f(3)=3!=3 2! =6
　　……
　　f(n)=n!=n (n-1)! n f(n-1)
　　要计算15！，可以从递推初始条件f(0)=1出发，应用递推通项公式f(n)= n f(n-1)逐步求出f(1)、f(2)、f(3)、…、f(14)，即由简到繁逐次迭代，直到最后求出f(15)的值。
　　递推法的关键是找到进行递推的通项公式，求一个数的阶乘是一个简单问题，该通项公式f(n)= n f(n-1)可以直接看出来。但事实上，有些问题要找出通项公式是相当困难的，并且即便找到计算也并非简便。这里我们只介绍递推法的基本思想方法，本书在第九章将对递推法和递归法进行较详细的讨论。
　　递归法：
　　什么是递归法？它与递推法有什么不同？递归法也是利用递推公式，所不同的是，它是由繁化简，用简单的问题和已知的操作运算来解决复杂的问题。仍以例1-7为例：
　　f(1)=1
　　f(n)= f(n-1)n
　　将后一个式子从n到n-1、再到n-2逐步递推化简得到：，
　　f(n)= f(n-1)n= f(n-2)(n-1)n
　　=…=f(1) 2 3 … n (n>1)
　　每一次化简，自变量减1，但要多乘一个因子。在化简的每一步，f(n-1)，f(n-2)，…等仍为未知量，直到化简到f(1)，则因为f(1)已知，f(n)便可由最后一个式子求乘法得到。这个计算过程不是直接的，它包含两个过程：
　　① 由繁到简的递推化简；
　　② 由已知值f(1)经乘法运算回归到所求值。
　　可见，递推与递归是有区别的。
　　通常递归是这样定义的：如果一个过程直接或间接地有限次数地调用了它自身，则称这个该过程是递归的。

　　例1- 8：有如下递归定义函数：

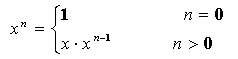　 由函数的定义可见，如果n=0， xn的值是1，如果n>0， xn的值就是xn-1的x倍。用递归法分析：对于任何大于0的整数n，xn的值是由xn-1的值确定的，而xn-1的值是由xn-2的值确定的，……，就这样逐次上溯调用其本身的求解过程，最终xn的值将归结到x0的定义上。而x0的定义是函数明确给出的，所以问题得到了结果。这就是递归的方法。
　　我们注意到在这个函数的右边使用了被定义形式xn本身，这就是"递归"这个词的意义。这种情况就是调用了它自身。
　　递归法的关键是必须有一个递归终止条件，即要有递归出口。无条件的递归是毫无意义的。上述函数的递归终止条件是n=0，这就是递归出口。在阶乘的递归定义中，当n=0时，n!=1也是阶乘递归定义的递归出口。
　　递归与递推是既有区别又有联系的两个概念。递推是从已知的初始条件出发，逐次递推出最后所求的值。而递归则是从需要求解的函数本身出发，逐次上溯调用其本身的求解过程，直到递归的出口，然后再从里向外倒推回来，得到最终的值。一般说来，一个递推算法总可以转换为一个递归算法。
　　一般而言，递推算法可利用循环结构实现，比较简单。而递归算法则要求语言具有反复自我调用子程序的能力，有些高级语言不具有这种能力，如FORTRAN、BASIC等。递归算法往往比非递归算法要付出更多执行时间，但尽管如此，因有很多问题的数学模型或算法设计方法本来就是递归的。用递归过程来描述它们不仅非常自然，而且证明算法的正确性也比相应的非递归形式容易很多，因此，递归仍不失为一种强有力的算法设计方法。
　　递归的概念首先在数学领域出现，然而，按递归方法设计算法的策略不仅适用于计算数学问题，而且也适用于非数值运算领域。例如检索过程的求解等。

4.分治法
　　在求解一个复杂问题时，应尽可能地把这个问题分解为较小部分，找出各部分的解，然后再把各部分的解组合成整个问题的解，这就是所谓的分治法。
使用分治法时，往往要按问题的输入规模来衡量问题的大小。若要求解一个输入规模为n且它的取值又相当大时，应选择适当的设计策略，将n个输入分成k个不同的子集合，从而得到k个可分别求解的子问题，其中k的取值为1<k≤n。在求出各个子问题的解之后，就可找到适当的方法把它们合并成整个问题的解。这里要注意的是，子问题要独立、要尽可能小。如果得到的子问题相对来说还太大，则可再次使用分治法进行分解。割得更小。
　　分治法常用于解决非数值运算问题，在数据检索、快速分类选择等问题的算法中被广泛应用

上一页  [1] [2] [3] [4]